Euler has been described as the "Mozart of maths". His most famous equation links all the most important numbers
"Most of modern mathematics and physics derives from work of Leonhard Euler," says Robin Wilson of the Open University in the UK. He was "the most prolific mathematician of all time" and "the Mozart of mathematics". But for all his achievements, "many so-called educated people have never heard of him."
His most famous single equation is Euler's identity. It is said to be the equation that can link all of the constants of mathematics together.
The equation combines five of the most important numbers in mathematics. These are:
1 – the basis of all other numbers
0 – the concept of nothingness
π (pi) – the number that defines a circle
e – the number that underlies exponential growth
i – the "imaginary" square root of -1
Understanding how e^(iπ) + 1 can equal zero is more difficult.
To begin to understand how to evaluate Euler’s Identity we must first understand about series expansions. The series expansion of a function can be used to calculate the value of this function to an arbitrary degree of precision.
The series expansion of e^x is given by:
If only the first term is used then e = 1.00, if two terms are used e = 2.00, if three terms are used e = 2.50, if four terms are used e = 2.66, and so on, until an infinite number of terms are used and the exact value of e is given. After only ten terms the value found for e is accurate to better than one part in a million.
The series expansion of e^(iπ) is therefore given by:
There are two other important expansions, the expansion of sin(x) and cos(x), two basic trigonometric functions.
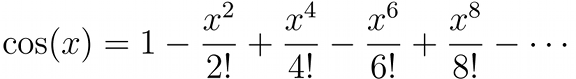
If we collect the terms in the expansions of sin(x) and cos(x) and compare them with the expansion of e^(ix) we find that:
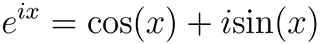
Inserting π in place of x in that expression yields:
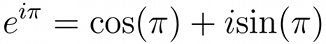
Because cos(π) = −1 and sin(π) = 0 we find that indeed, e^(iπ) = −1 and therefore:
References:
1- BBC - Earth article
By Melissa Hogenboom
20 January 2016
2- MrReid.org
Comentários